Betekintés a sejtautomaták világába Processing segítségével - Bevezetés

Sejt, sejttér:

• Itt most egy négyzetrács celláit nevezzük sejteknek, az összességüket pedig sejttérne.
• Ezen négyzetrács lehet n*1 méretű avagy 1 dimenziós, n*m méretű avagy 2 dimenziós, n*m*v méretű avagy 3 dimenziós..

---

Állapot:

• A sejtek véges sokféle állapotban lehetnek, amik színekkel remekül ábrázolhatók. Pl. ki (0, fehér) és bekapcsolt (1, fekete) sejt.

---

Szomszédság:

• Avagy távolság a vizsgált sejttől, mely sejtek hatnak rá. (a sejttől átlós elemeket is egy távolságbanlévőnek tekintjük a tőle eggyel fentebb, lentebb, balra vagy jobbra levőkkel)
• Ezt egyébként Moore szomszédságnak nevezik. A szomszédság több híres meghatározzásról, köztük a Neumann szomszédságról itt található bővebb információ.

Szomszédságok

Súgó

A különböző szomszédságokat bemutató képek, az X-el jelölt cella jelzi a vizsgált elemet.

Dimenzió	1-es szomszédság	2-es szomszédság
1D, egyenes
2D, sík

Iteráció, generációk, avagy az idő múlása:

• A sejttér minden sejtjének állapotát módosítjuk a rá vonatkozó szomszédsági szabályoknak megfelelően, így megkapjuk a következő generációt avagy időbeli állapotot.

Keltsük életre az automatát!

Nyissuk meg egy üres projektet a Processing-ben és illesszük be a következő kódot:

final int cellsPerRow = 200; // soronkénti cellák száma >= 2
int[] cells;                 // a cellák 0 vagy 1 értékkel
final int RULE = 99;         // A szabály

void setup() {
    size(800,1000, P2D); // Ablak mérete
    
    // Inicializásió
    cells = new int[cellsPerRow];
    int side = width / cellsPerRow;

    for (int i = 0; i < cellsPerRow; i++) 
    cells[i] = 0;
    
    cells[cellsPerRow/2] = 1; // Egy aktív cella középen
    
    // A képernyő kitöltése
    for(int i = 0; i < height / side; i++) {
    drawCells(i, side);
    iterate();
    }
    
}

void iterate() { // A következő generáció
    int[] cells2 = new int[cellsPerRow];
    
    cells2[0] = (RULE >> (cells[0] * 2 + cells[1] * 4)) & 1;
    cells2[cellsPerRow-1] = (RULE >> (cells[cellsPerRow-2] + cells[cellsPerRow-1] * 2)) & 1;
    
    for (int i = 1; i < cellsPerRow - 1; i++) {
    cells2[i] = (RULE >> (cells[i-1] + cells[i] * 2 + cells[i+1] * 4)) & 1;
    }
    
    for (int i = 0; i < cellsPerRow; i++) 
    cells[i] = cells2[i];
}


void drawCells(int generation, int side) { // Felrajzol egy generációt
    noStroke();
    for (int i = 0; i < cellsPerRow; i++) {
        if (cells[i] == 1) fill(0);
        else fill(255);
        
        rect(i * side, side * generation, side, side);
    }
}

Sejtenként a szomszédsági szabályt a következő képlettel számítom ki:

(RULE >> (cells[i-1] + cells[i] * 2 + cells[i+1] * 4)) & 1;

A RULE címen tárolt egész számnak egyetlen bitjét kéri le a három szomszédos cella értékéből képzett 0-7 terjedő számmal. A cells tömb széleinél a szomszédsági szabály kiszámátásához 0 állapotúnak veszem a hiányzó elemeket.

Kisérletezz a szabályokkal és a kezdőállapotokkal! Milyen érdekes formákat tudsz felfedezni?

Hogy lehetne megoldani, hogy a páratlan szabályoknál ne csússzon el minden második sor széle?

Személyes kedvenceim:

1 + 1 dimenzió, 1-es szomszédság

Súgó

Pár kiemelt szabály és a fentebbi program futtatásával a velük generálható képek

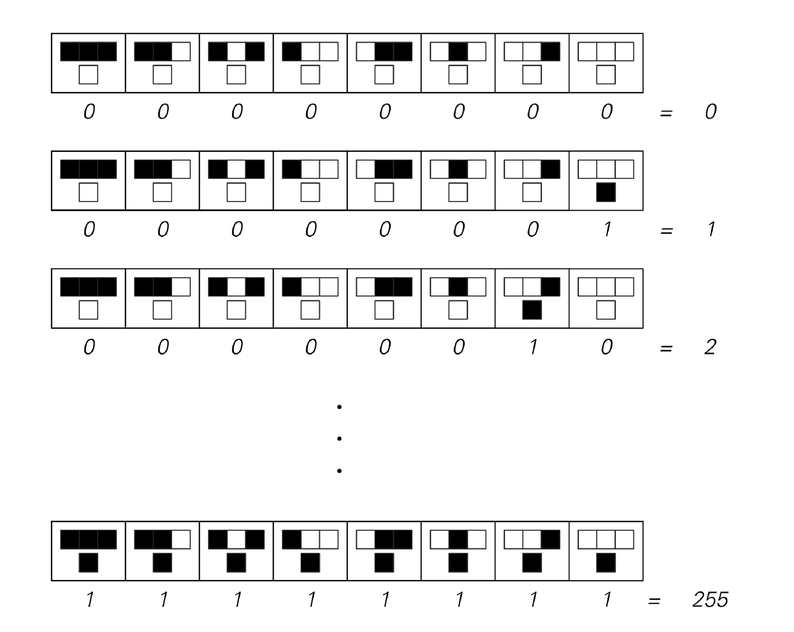
Az 1*n méretű négyzetrácsos sejttéren, 2 állapotú, 2-es szomszédsággal megvalósítható automaták:

Vajon mennyivel lesz több szabályunk, ha a szomszédságot eggyel növeljük?

Mint ahogy az fentebb már látható, a szabályok száma finoman szólva is drasztikusan megugrik! Egy 32 bites egész szám összes bitjére szükségünk lesz, hogy minden ilyen autoamatát megadhassunk.

Kettő jobb és kettő bal szomszéd + maga a sejt: 5 elem

Két állapot sejtenként: 0 vagy 1

=> 2^5 = 32 esetre kell megadnunk, hogy a következő generációban a vizsgált sejt helyén 0-s vagy 1-es legyen, így esetenként megint 2-2 opciónk van.

(2^5)^2 = 2^32 = 2147483647

Összesen 2147483647 szabállyal adható meg minden ilyen autómata működése.

Az egymást követő generációkat megint egymás alá rajzoljuk, így marad az 1 tér(x) + 1 idő(y) dimenzió.

Az előző kód egy kis módosítással képes lesz a 2-es szomszédságú automaták szimulálására is:

void iterate2() { // A következő generáció
  int[] cells2 = new int[cellsPerRow];

  cells2[0] = (RULE >> (cells[0] * 4 + cells[1] * 8 + cells[2] * 16)) & 1;
  cells2[1] = 
    (RULE >> (cells[0] * 2 + cells[1] * 4 + cells[2] * 8 + cells[3] * 16)) & 1;

  cells2[cellsPerRow-1] = 
    (RULE >> (cells[cellsPerRow-3] * 1 + cells[cellsPerRow-2] * 2 + cells[cellsPerRow-1] * 4)) & 1;

  cells2[cellsPerRow-2] = 
    (RULE >> (cells[cellsPerRow-4] * 1 + cells[cellsPerRow-3] * 2 + cells[cellsPerRow-2] * 4 + cells[cellsPerRow-1] * 8)) & 1;


  for (int i = 2; i < cellsPerRow - 2; i++) {
    cells2[i] = (RULE >> (cells[i-2] * 1 + cells[i-1] * 2 + cells[i] * 4 + cells[i+1] * 8 + cells[i+2] * 16)) & 1;
  }

  for (int i = 0; i < cellsPerRow; i++)
    cells[i] = cells2[i];
}

A setup() metódusban hívjuk meg az iretare2() függvényt az itarate() helyett.

// A képernyő kitöltése
for(int i = 0; i < height / side; i++) {
  drawCells(i, side);
  iterate2();
}

Ezen a ponton már érdemes lenne nem manuálisan módosítani a RULE változó értékét. Sorsoljuk egy véletlen szabályt!

1. Importáljuk be a Random osztályt a következő sor beillesztésével a kódunk tetejére:

   Random rand = new Random();

2. Adjunk hozzá a projekthez egy üres draw() metódust, hogy annak futása ne álljon le egy szabály rajzolása után!

   void draw() {}

3. A következő metódus megírásával kössük össze mondjuk az R billentyű lenyomását egy véletlenszerű szabály kisorsolásával és megjelenítésével!

void keyPressed() {
  if (key == 'r' || key == 'R')
    RULE = rand.nextInt();

  println(RULE);
  
  setup();
}

Így kaphatunk akár ilyen részletekben és mintákban gazdag képeket:

1 + 1 dimenzió, 2-es szomszédság

Súgó

Ízelítő a fentebbi program 2-es szomszédsággal módosított változatával kapott képekből